Underlying Architecture 🌱
Most programs work and process information the same way.
- 🦆 operating system
- 🗃️ databases
- 🔦 programming languages
- ...
This section gathers fundamental concepts to understand how systems operate at low-level/near the machine.
This includes topics such as:
- 📦 Signed or Unsigned; Little- or Big- endian...
- 🍎 Types, arithmetic, overflow, machine representation
- ...
Numbers 🔢
While systems typically offer types such as boolean, integer, float, and string, for a machine, there are usually 4 types:
- bit: 0 or 1. Often used for booleans.
- byte: 8 bits.
- word: width of a register. 16, 32, or 64 bits (modern computers).
- dword (double word): usually 32 or 64 bits
Refer to the Encoding | Binary to learn more about how numbers are represented using 0 and 1.
Signed or unsigned?
Numbers can be signed or unsigned. If a number is signed, it means that the first bit is the sign: $0$ = positive, $1$ = negative.
Given $n$ bits, we can represent values between
- $[2^{n-1}, 2^{n-1}-1]$ for a signed number
- $[0, 2^{n} - 1]$ for an unsigned number
👉 The position of the first bit is determined by the data type.
Endianness
Numbers are stored and read according to the endianness of the machine. For instance, given $(10)_2$
- Big endian: we will store/read $1$ then $0$
- Little endian: we will store/read $0$ then $1$
The same number could have two different values according to the endianness of the one that stored it, and the one that read it.
👉 This does not include the sign bit whose position is fixed.
Arithmetic operations
Operations are between positive binaries. You will have to use the two's complement to use negative values in operations.
The only operation possible is the addition. a-b is handled as a+(-b).
Two's complement - negative numbers
The two's complement is an "upgrade" to the One's complement, which has the default of having two representations for the number zero. It's as simple as that:
- Invert all bits
- Add 1
Example of addition
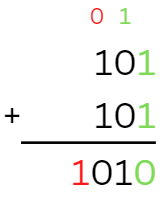
To add 5 (101) to 5 (101), you need to do it like you would in grad school, with a carry.
- $1+1=0$ with $carry={\color{cyan}1}$
- $0+0+{\color{cyan}1}=1$ with $carry={\color{red}0}$
- $1+1+{\color{red}0}=0$ with $carry={\color{orange}1}$
- $0+0+{\color{orange}1}=1$ with $carry=0$
Problems
- 🔥 Overflow: an overflow occurs when the result of a calculation is outside the range of values that can be stored with our number of bits. An overflow is without consequences if the result is valid.
Floating-point numbers
A floating-point number can be identified by the decimal point (a.k.a. radix point), which is usually either . (dot), or , (comma).
Fractional part
Similarly to the scientific notation $x * 10^n$ in decimal, a computer represents a fraction part a $y * 2^m$.
➡️ Not every number can be written using scientific notation
- $e(a)$ extracts the digits after the radix point of $a$ (ex: 1.11 $\to$ 0.11)
- $a_i = \text{your_number}$
- do
- $a_i = e(a_i) * 2$
- $r_i = \text{if}\ a_i > 1.0\ \text{then}\ 1\ \text{else}\ 0$
- while $a_i \neq 1.0$
Then concatenate every $r_i$ to get the floating-point representation in binary. For instance, with $.75$
- $a_0 = 0.75 * 2 = 1.5$
- $r_0 = 1$
- $a_1 = 0.5 * 2 = 1.0$
- $r_1 = 1$
Giving us: $.75=(.11)_2$.
Binary-coded Decimal (BCD)
Binary-coded decimal, a.k.a. decimal-coded binary (DCB), is used to store a fixed-length floating-point number. It's not used aside from in financial institutions or when we need to store monetary values, as there is no loss of precision, but it takes more space.
Each value is stored in 4 bits. For the fractional part, we use the method above.
In databases, we often use the type: decimal(n,m). It means n digits, and m fractional part numbers.
➡️ In Packed BCD, we convert each block to hexadecimal, which is more space-efficient, but less usage-efficient (need to unpack...).
IEEE754
IEEE754 is the norm modern computers are using to store a floating-point number. 3 integers are needed to do so:
| float (32 bits) | double (64 bits) | |
|---|---|---|
|
S: the sign, 0=positive, 1=negative | 1 bit | |
|
E: exponent bias | 8 bits | 11 bits |
|
M: significand, mantissa, or coefficient | 23 bits | 52 bits |
| $q = 127$ | $q=1023$ | |
As $5 = (101)_2$, and $.75=(.11)_2$, we have $(5.75)_{10}=(101.11)_2$.
You should have noticed that we have "1.M", so we have to move the radix point by 3 times to the left, giving us $(101.11)_2 = (1.0111)_2 * 2^3$.
Example 🔥: from a decimal to a float (simple precision):
- $S = 0$, because $5$ is positive
- $E = 130$: we had to solve $E - q = 3$, with $3$ the shift amount, and $q=127$ as we are using simple precision
- $M = 0111$, as our number is $1.0111$, $M$ is the fractional part
Example 🔥: from a float to a decimal
To find back numerical value, evaluate $(-1)^S * 1.M * 2^{E - q}$.
Problems
- loss of precision 💦: numbers are truncated. For instance, adding a small number to a big number, may result in the same big number, unchanged ($a + \xi = a$).
- not associative 🌾: $(a+b)+c$ may not be equals to $a+(b+c)$, mostly because of truncating.
- overflow: same as for integers overflow.
Strings 💬
A string is an array of characters, such as 'a'. A string could have a fixed length, or a variable length. For the latter, we may use a null character such as \0 to mark the end.
A character is encoded to a number following a charset, as we can only store integers. Some charsets are ASCII, UTF...
ASCII table (7 bits)
The ASCII table is the most well-known table. 'a' in ASCII is the number 97. 7 bits are not enough to store every character, so it's less used than in its prime.
Extended ASCII table (8 bits)
This is an extension of the ASCII table adding 128 characters. It is NOT fixed. It means that given a character such as 130, there is no warranty that all extended tables will have the same character for it.
Unicode (UTF)
UFT-8 and other variants are mainly used in international applications. UTF-8 characters are stored in 4 bytes.
Fonts
A font is a set of glyphs to render a character. Given two fonts, one could render the letter 'a' as a while another could render it as +.
Collation (database)
This is a set of rules defining how characters are ordered, compared, how the case is handled (is it case-sensitive?), and how special characters are treated (à==a? before "a"? after "a"?).
Others
Null value
There is usually a null value to indicate that something exists but is empty. In most languages, it's NULL or null.
Not A Number
There may be a value to indicate that a value is not a number. For instance, 1/0. It's usually NaN.
Size
- 1 Kb (kilobyte): $2^{10} = 1024$
- 1 Mb (megabyte): $2^{20} = 1,048,576$
- 1 Gb (gigabyte): $2^{30} = 1,073,741,824$
- 1 Tb (terabyte): $2^{40} = 1,099,511,627,776$
- ...
Dates
Most dates are a number of seconds/milliseconds since a starting point/epoch. In many languages/systems, it is the 1st of January 1970.
In some applications/systems, the number may be a number of days. To represent the time, We add a fraction of the day to the number of days. For instance, 12 h = 1/2, so the day of epoch (0) at 12 h (.5) would be 0.5.
👻 To-do 👻
Stuff that I found, but never read/used yet.
- Little Man Computer (LMC)
- Hypervisor: software to run VMs. Virtually sharing memory and processing resources. Isolated from OS.

