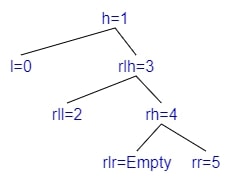
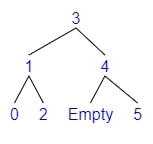
AVL trees
An AVL (Adelson-Velsky and Landis) is a balanced Binary Search Tree. We will ensure that there is no more than one level of "depth" between branches. The complexity is now $\log{(n)}$.
This is an example of a bad BST ($O(n)$) :
Everything is the same as for a Binary Search Trees, but we will call a function to balance our tree after add and remove.
Only the implementation of the said function is explained here.
- ✅: faster than an ordered list for
add, remove - ✅: better than an unbalanced BST
- ✅: implementation is mostly the same as for a BST
- ❌: add and remove are difficult to understand/implement
- ❌: slightly slower than an ordered list for
mem,get_min
Time comparisons - 500 000 values between 0 and 10 000
Test results of an implementation in OCaml.
>>>>>>>>>> TIME FOR A LIST <<<<<<<<<<
Average time of add: 0.000046
Average time of remove: 0.000047
Average time for mem: 0.002340
Average time for get_min: 0.001870
Average time for cardinal: 0.353290 (long)
>>>>>>>>>> TIME FOR BST <<<<<<<<<<
Average time of add: 0.000002
Average time of remove: 0.000002
Average time for mem: 0.006270
Average time for get_min: 0.003290
Average time for cardinal: inf (too long)
>>>>>>>>>> TIME FOR AVL <<<<<<<<<<
Average time of add: 0.000010
Average time of remove: 0.000005
Average time for mem: 0.003430
Average time for get_min: 0.002800
Average time for cardinal: inf (too long)
Rotations
Each time we add an element (parent node determined by the algorithm), we may have to correct imbalances using one of the 4 patterns below:
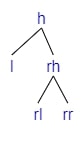 Left Rotation
Left Rotation
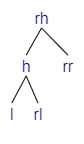
If we are adding a child to rr.
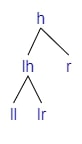 Right Rotation
Right Rotation
If we are adding a child to ll.
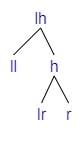
 Inserting in lr
Inserting in lr
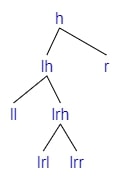 Apply Left Rotation
Apply Left Rotation
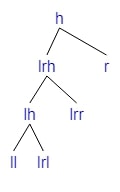 Apply Right Rotation
Apply Right Rotation
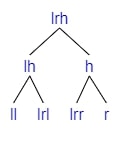
If we are adding a child to lr (=lrh if lr is empty, otherwise either lrl or lrr).
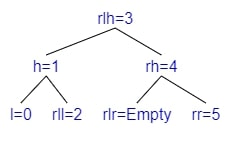
 Inserting in rl
Inserting in rl
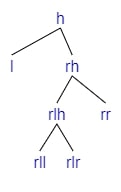 Apply Right Rotation
Apply Right Rotation
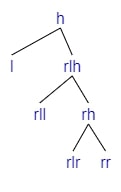 Apply Left Rotation
Apply Left Rotation
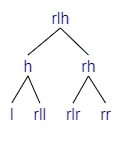
If we are adding a child to rl (=rlh if lr is empty, otherwise either rll or rlr).
Balancing Algorithm
The height means the length of the longest path from that node to a leaf. The Balance factor of a node bf(node) is the difference of height between two branches (left child node minus right child node).
Find where the tree is unbalanced
Calculate the balance factor of the root:
-
bf(root) = 2: the tree is left-balanced -
bf(root) = 2: the tree is right-balanced - Otherwise, do nothing
Correct a left-balanced tree
-
bf(right) = 1: Apply a Rotate Right Left -
bf(right) = 0: ❌ (impossible) -
bf(right) = -1: Apply Rotate Left
Correct a right-balanced tree
-
bf(left) = 1: Apply a Rotate Right -
bf(left) = 0: ❌ (impossible) -
bf(left) = -1: Apply Rotate Left Right
Example 1 - Rotate Left
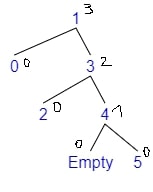
- Adding 5
- $bf(tree) = depth(left) - depth(right) = 0 - 2 = -2$
- The tree is Right balanced
- $bf(right) = depth(r\_left) - depth(r\_right) = 0 - 1 = -1$
- Rotate Left
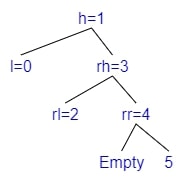
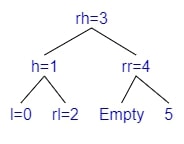
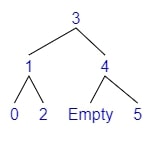
Example 2 - Rotate Right
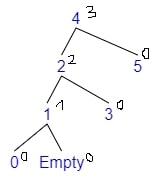
- Adding 0
- $bf(tree) = depth(left) - depth(right) = 2 - 0 = 2$
- The tree is Left balanced
- $bf(left) = depth(l\_left) - depth(l\_right) = 1 - 0 = 1$
- Rotate Right
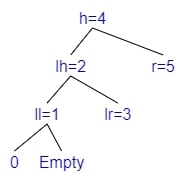
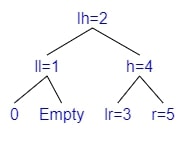
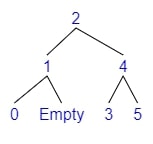
Example 3 - Rotate Left Right
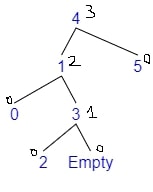
- Adding 2
- $bf(tree) = depth(left) - depth(right) = 2 - 0 = 2$
- The tree is Left balanced
- $bf(left) = depth(l\_left) - depth(l\_right) = 0 - 1 = -1$
-
Rotate Left Right
- We will Rotate Left the left
- We will Rotate Right the tree
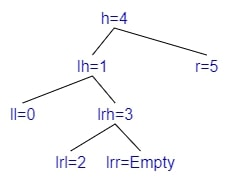 Left Rotation
Left Rotation
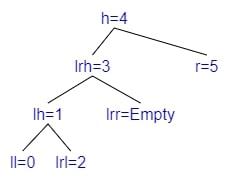 Right Rotation
Right Rotation
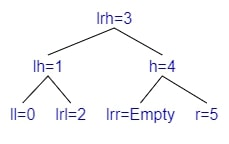
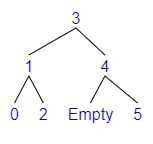
Example 4 - Rotate Right Left
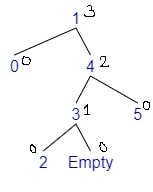
- Adding 2
- $bf(tree) = depth(left) - depth(right) = 0 - 2 = -2$
- The tree is Right balanced
- $bf(right) = depth(r\_left) - depth(r\_right) = 1 - 0 = 1$
-
Rotate Right Left
- We will Rotate Right the right
- We will Rotate Left the tree
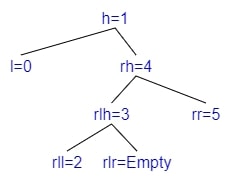 Right Rotation
Right Rotation
 Left Rotation
Left Rotation