Graph Coloring Problems Examples

Vertex coloring Greedy Algorithm Example

Use the Welsh-Powell greedy algorithm and find the coloration for the following graph. Is it the optimal solution?

Vertex coloring Greedy algorithm Example Graph

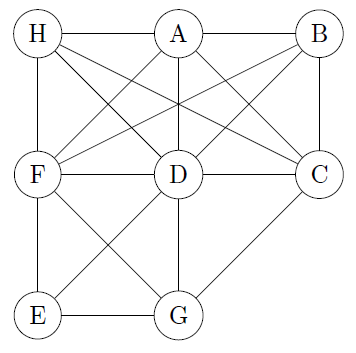
  • $d(D)=7$
  • $d(F)=6$
  • $d(A)=d(C)=5$
  • $d(B)=d(G)=d(H)=4$
  • $d(E)=3$

Giving us the following table:

Colors\Vertex D F A C B G H E
Red o x x x x x x x
Yellow o x o x x x x
Green o x x o x
Blue o o o
  • o=colored
  • x=not colored since neighbor to a colored
  • "nothing"=already colored

The longest clique is $D-C-A-H$ (size=4) and we colored the graph in $4$ colors, so this is the optimal solution. We had the clique $F-D-G-E$ too.

Vertex coloring Contraction Algorithm Example

Use the contraction algorithm to find a coloration for this graph:

Vertex coloring Contraction Algorithm Example Graph

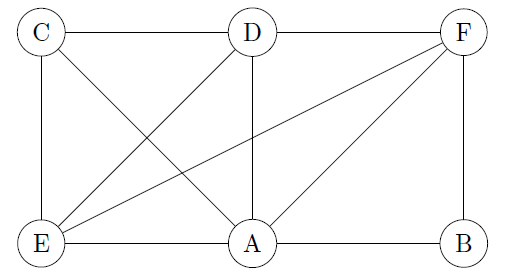
We have 4 missing edges, so we will have up to $2^4=16$ subgraphs. We are missing the following edges: $[c,b], [d,b], [e,b], [c,f]$.

Vertex coloring Contraction Algorithm Example Graph Corrected

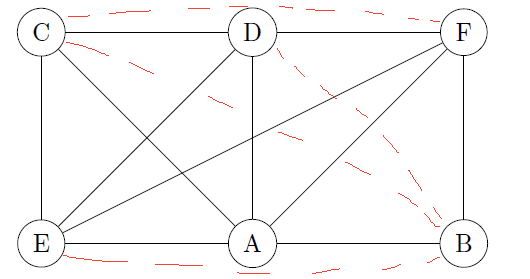
Let's apply the algorithm (note: C=Contraction, L=Link=Connect):

Vertex coloring Contraction Algorithm Example Algorithm

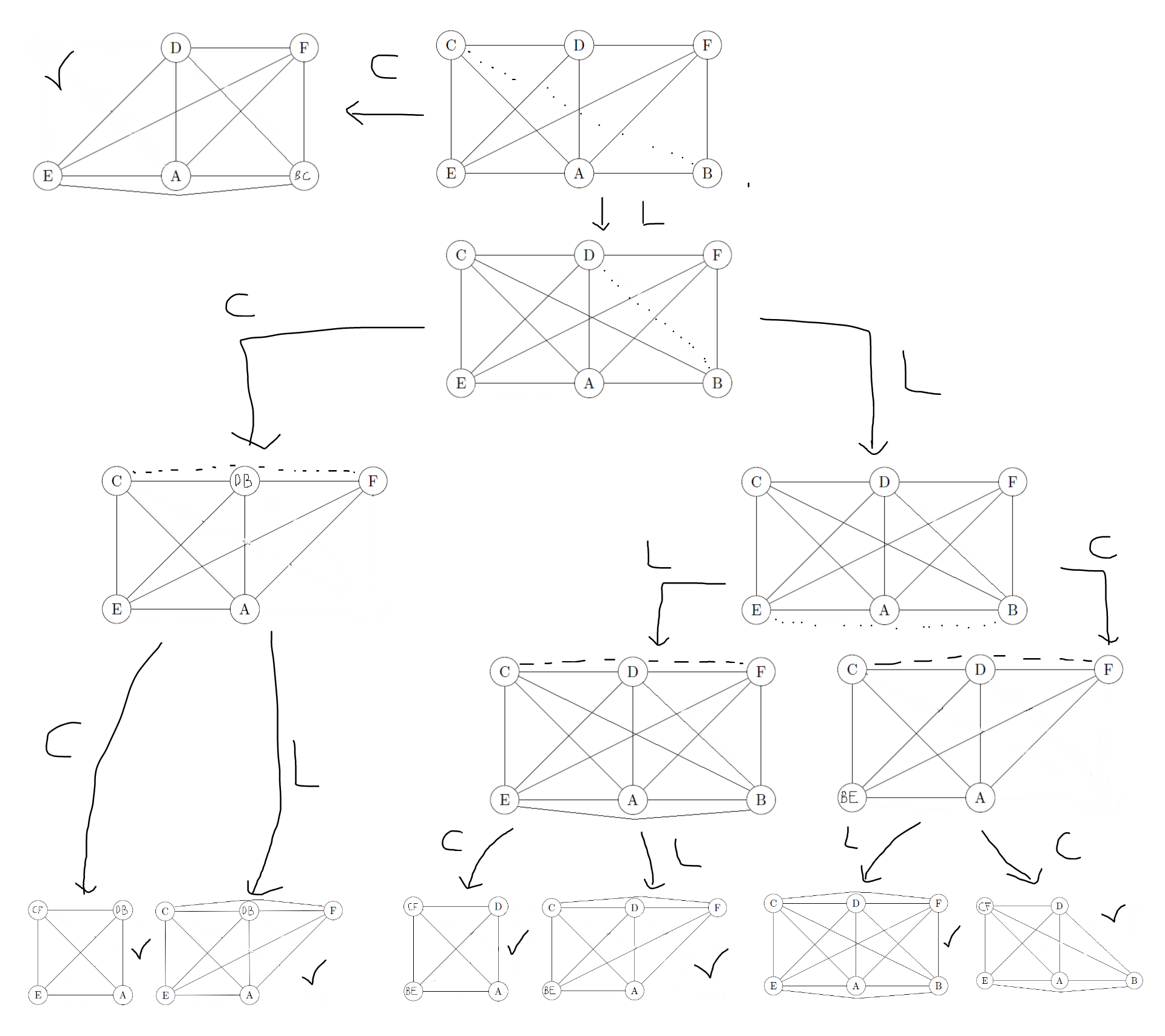
The smallest clique among the 7 graphs with the symbol ✔️ is:

  • $CF-DB-E-A$: 4 colors
  • $CF-D-BE-A$: 4 colors

It means one way to color the graph is:

Vertex coloring Contraction Algorithm Example Result

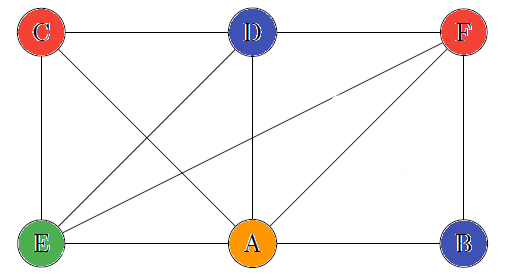
Grundy Function Example 1

Use Grundy on the following graph $G$:

Grundy Function Example 1 Graph

Using Grundy function, starting from $1$, we have:

Grundy Function Example 1 Answer

  • The first one is in the kernel, so $g(1)=0$
  • Next is the successor $2$
    • the neighbors took the values $\text{{0}}$
    • the lowest value we can give is $1$
    • $g(2)=1$
  • Next are the successors $3,5$
    • ... $\text{{1}}$, the lowest ... $0$
    • $g(3)=0$ and $g(5)=0$
  • Next is the successor $4$
    • ... $\text{{0}}$, the lowest ... $1$
    • $g(4)=1$
  • Next is the successor $6$
    • ... $\text{{0}}$, the lowest ... $1$
    • $g(6)=1$

We got the kernel $(1,5,3)$. Starting from another vertex like $4$, we would have found the other kernel $(2,4,6)$.

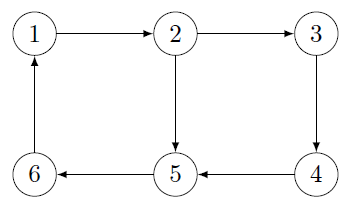
Grundy Function Example 2

Find a kernel for this graph using the grundy function

Grundy Function Example 2 Graph

Vertex $1$ does not have any predecessors, so we must start at $1$.

Grundy Function Example 2 Answer

Then:

  • $g(2)=g(4)=1$ because $g(1)=0$
  • $g(2)=2$ because we have the predecessors already have:
    • $g(1)=0$
    • $g(4)=1$
  • Then we have a choice (=two kernels)
    • $g(5)=0$ and $g(3)=1$
    • $g(3)=0$ and $g(5)=2$

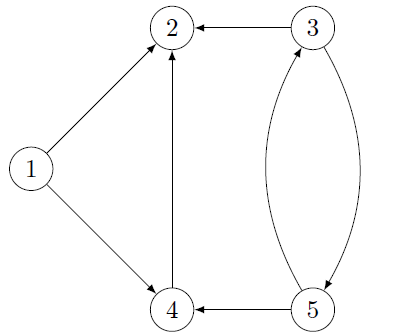
Grundy Function Example 3

Find a kernel for this graph using the Grundy function after sorting the vertices by successors.

Grundy Function Example 3 Graph

Let's sort the vertices:

  • $3$: 0 successor
  • $5$: 1 successor
  • $7$: 1 successor
  • $8$: 1 successor
  • $1$: 2 successors
  • $2$: 2 successors
  • $4$: 2 successors
  • $6$: 4 successors

And the result is:

Grundy Function Example 3 Answer

  • $g(3)=0$ (no successors $\to$ should be the start, inside the kernel)
  • $5$ is not a neighbor of $3$: $g(5)=0$
  • $7$ is not a neighbor of $3,5$: $g(7)=0$
  • $8$ is a neighbor of $g(3)=0$: $g(8)=1$
  • $1$ is a neighbor of $g(3)=0, g(5)=0$: $g(1)=1$
  • $4$ is a neighbor of $g(3)=0, g(8)=1$: $g(4)=2$
  • $2$ is a neighbor of $g(5)=0, g(4)=2$: $g(2)=1$
  • $6$ is a neighbor of $g(1)=g(2)=g(8)=1, g(7)=0$: $g(6)=2$

The kernel is $3,5,7$.

Grundy Function Example 4

Given this adjacency matrix, calculate the Grundy function.

Grundy Function Example 4 Graph

Let's sort the vertices

  • $0$: 2 successor
  • $1$: 3 successor
  • $2$: 2 successor
  • $3$: 1 successor
  • $4$: 2 successor
  • $5$: 1 successor
  • $6$: 1 successor
  • $7$: 1 successor
  • $8$: 0 successor

Giving us $8-3-5-6-7-0-2-4-1$.

  • $g(8)=0$ (no successors $\to$ should be the start, inside the kernel)
  • $7$ is a neighbor of $g(8)=0$: $g(7)=1$
  • $5$ is a neighbor of $g(7)=1$: $g(5)=0$
  • $3$ is a neighbor of $g(5)=0$: $g(3)=1$
  • $6$ is a neighbor of $g(7)=1$: $g(6)=0$
  • $4$ is a neighbor of $g(8)=g(6)=0$: $g(4)=1$
  • $2$ is a neighbor of $g(7)=1, g(5)=0$: $g(2)=2$
  • $1$ is a neighbor of $g(2)=2, g(3)=g(4)=1$: $g(1)=0$
  • $0$ is a neighbor of $g(1)=0, g(4)=1$: $g(0)=2$

The kernel is $1,5,6,8$.

Note: we processed $7$ before $3$/$5$ because both depended on it.