Graph Properties and Concepts Examples
Connected Graph Example
Given the following graph $G$:
What are the connected components?
We have $C_1={e,f,g}$ and $C_2={a,b,c,d,h,i}$ using the algorithm.

Is the graph connected?
No, we have more than one connected component.
Create a subgraph $G'$ with $\text{{a,b,c,d}}$.
We extract the vertices and their edges.
Is $G'$ connected? And super-connected?
We only have one component, so the graph is connected. The graph does seem to be super-connected. We apply the algorithm:

All vertices are marked with "+" and "-", the graph is super-connected.
Transitive closure and Connectivity Example
Use the transitive closure to determine if $G$ is super-connected.
Using Roy-Warshall's algorithm, we got the transitive closure:
This is a complete graph $K_{6}$. Since the transitive closure is a complete graph, then $G$ is super-connected.
For reference, here is Roy-Warshall's algorithm:

The complete algorithm (text)
- picking A
- $s=C$, $p=B$, creating (B,C)? yes
- $s=C$, $p=E$, creating (E,C)? yes
- $s=C$, $p=F$, creating (F,C)? yes
- picking B
- $s=A$, $p=C$, creating (C,A)? yes
- $s=A$, $p=F$, creating (F,A)? no
- $s=A$, $p=D$, creating (D,A)? yes
- $s=C$, $p=F$, creating (F,C)? no
- $s=C$, $p=D$, creating (D,A)? no
- picking C
- $s=B$, $p=A$, creating (A,B)? yes
- $s=B$, $p=D$, creating (D,B)? no
- $s=B$, $p=E$, creating (E,B)? yes
- $s=B$, $p=F$, creating (F,B)? no
- $s=E$, $p=A$, creating (A,E)? yes
- $s=E$, $p=B$, creating (B,E)? yes
- $s=E$, $p=D$, creating (D,E)? yes
- $s=E$, $p=F$, creating (F,E)? yes
- picking D
- $s=A$, $p=E$, creating (E,A)? no
- $s=B$, $p=E$, creating (E,B)? no
- $s=C$, $p=E$, creating (E,C)? no
- $s=E$
- $s=F$, $p=E$, creating (E,F)? no
- picking E
- $s=A$, $p=B$, creating (B,A)? no
- $s=A$, $p=C$, creating (C,A) ? yes
- $s=A$, $p=D$, creating (D,A)? no
- $s=A$, $p=F$, creating (F,A)? no
- $s=B$, $p=A$, creating (A,B)? no
- $s=B$, $p=C$, creating (C,B)? no
- $s=B$, $p=D$, creating (D,B)? no
- $s=B$, $p=F$, creating (F,B)? no
- $s=C$, $p=A$, creating (A,C)? no
- $s=C$, $p=B$, creating (B,C)? no
- $s=C$, $p=D$, creating (D,C)? no
- $s=C$, $p=F$, creating (F,C)? no
- $s=D$, $p=A$, creating (A,D)? yes
- $s=D$, $p=B$, creating (B,D)? yes
- $s=D$, $p=C$, creating (C,D)? yes
- $s=D$, $p=F$, creating (F,D)? yes
- $s=F$, $p=A$, creating (A,F)? yes
- $s=F$, $p=B$, creating (B,F)? yes
- $s=F$, $p=C$, creating (C,F)? yes
- $s=F$, $p=D$, creating (D,F)? no
- $s=F$
- picking F
- done
Planar Graph Example
Are the following graphs planar?
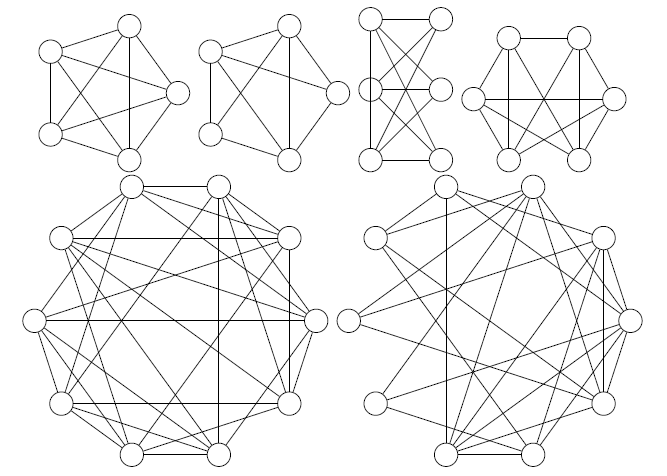
Planar Graph Example Graph 1
The first graph is planar because it's $K_5$.
Planar Graph Example Graph 2
The second one is planar as it has at least one planar representation.
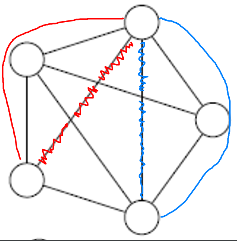
✅ $n + m = f = 2$ ($n=5$, $m=9$, $f=6$=five+the outer face).
Planar Graph Example Graph 3
A subgraph of the third graph is $K_{3,3}$ so it's not a planar graph.
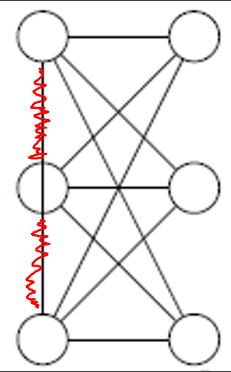
Planar Graph Example Graph 4
The fourth graph $m=12 \le 6 * 3 - 5 \le 13$, so the graph is planar. Simply move the vertices "4" and "5" to the locations I marked.
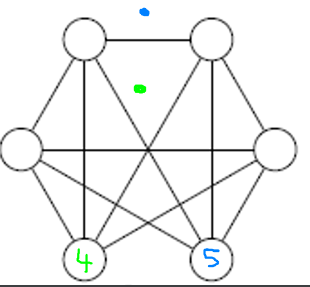
Planar Graph Example Graph 5
All degrees are equal to $6$, so the graph is not planar. Alternatively, we could have used the formula $m < 3n - 5$.
Planar Graph Example Graph 6
We can merge vertices and get the minor of the graph which is $K_6$. If we remove any vertex, we get the subgraph $K_5$. As per Robertson–Seymour theorem, it's not a planar graph.

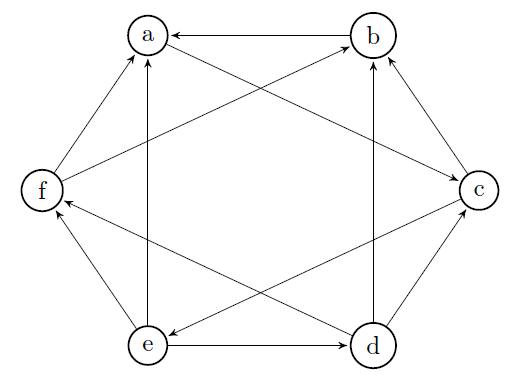
Cycle basis Example
Given the following graph:
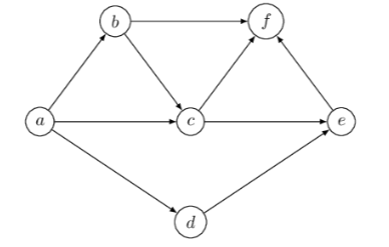
We will use the following ordered edges:
@ E = \{(a,b),(a,c),(a,d),(b,c),(b,f),(c,e),(c,f),(d,e),(e,f)\} @
What's the vector for $(bcfb)$?
$(bcfb) \to (0,0,0,1,-1,0,1,0,0)$.
- ...
- the 4th value is $1$ since $bc$ is in $bcfb$ in the same order
- the 5th value is $-1$ since $bf$ is in $bcfb$ ($fb$) in another order
- ...
What's the vector for $(abfeda)$?
$(abfeda) \to (1,0,-1,0,1,0,0,-1,-1)$.
$(bcfb)$ is a linear combination of 2 cycles. Which ones?
One answer would be $(bcfb) = (bcefb) + (ecfe)$.
What's $\mu(G)$?
$\mu(G) = m - n + p \Leftrightarrow 9-6+1 = 4$
Give a cycle basis $B$ which doesn't include both $(bcfb)$ and $(abfeda)$.
$B = \{(abca), (cfec), (acefba), (adeca)\}$
You must look for cycles that have an arc that is not in a cycle you already created, so that you are sure that can't get it by linear combination. Notice that we got $4$ cycles inside $B$, as calculated.
Co-cycle basis Exercise
Given the following graph:
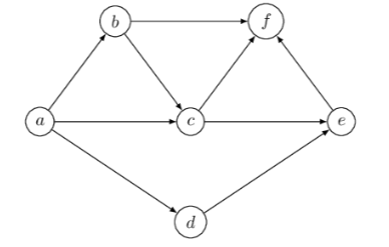
We will use the following ordered edges:
@ E = \{(a,b),(a,c),(a,d),(b,c),(b,f),(c,e),(c,f),(d,e),(e,f)\} @
What's the vector for $(abf)$?
$(abf) \to (0,1,1,1,0,0,-1,0,-1)$
- ...
- the $2^{nd}$ value $(a,c)$, $a$ is inside, $c$ outside so $1$
- ...
- the $7^{th}$ value $(c,f)$, $c$ is outside, $f$ inside so $-1$
- ...
What's the vector for $(ae)$?
$(ae) \to (1, 1, 1, 0, 0, -1, 0, -1, 1)$.
$(ae)$ is a linear combination of 2 co-cycles. Which ones?
Possible answer: $(ae) = (a) + (e)$ (because they are a stable set)
What's $\gamma(G)$?
$\gamma(G) = n - p \Leftrightarrow 6-1 = 5$
Give a cycle basis $B$ which doesn't include co-cycles of one vertex.
$B' = \{(abc), (bcf), (cfe), (aced), (abfed)\}$
Notice that we got $5$ co-cycles inside $B$, as calculated.
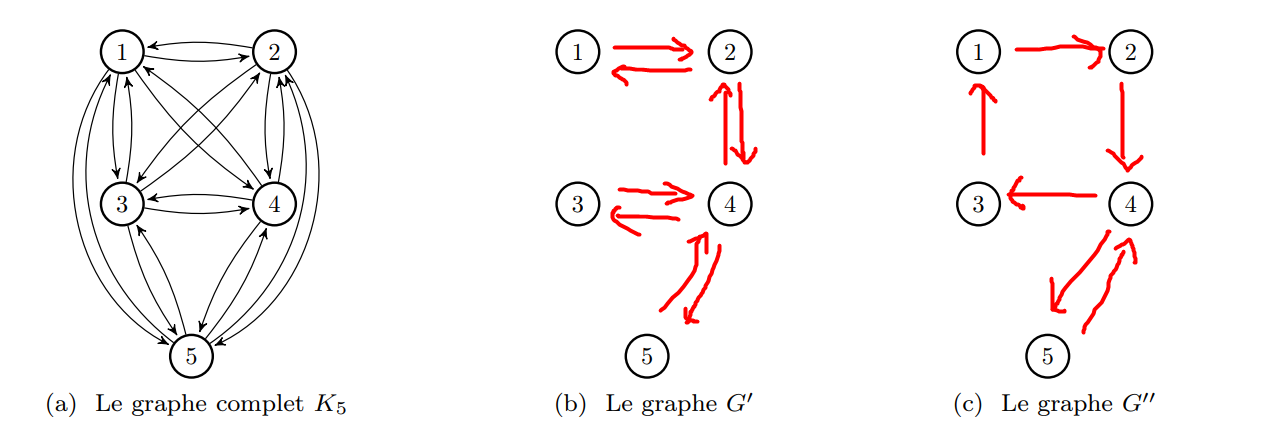
Spanning Subgraph Examples
Spanning Subgraph Example 1
Starting from the graph $G$, create:
- $G'$: $\tau$-minimal $\tau$-equivalent
- $G''$: $\tau$-minimum $\tau$-equivalent
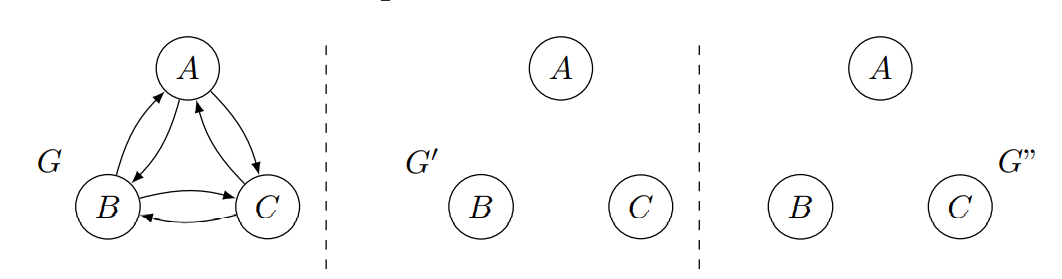
One possible answer:
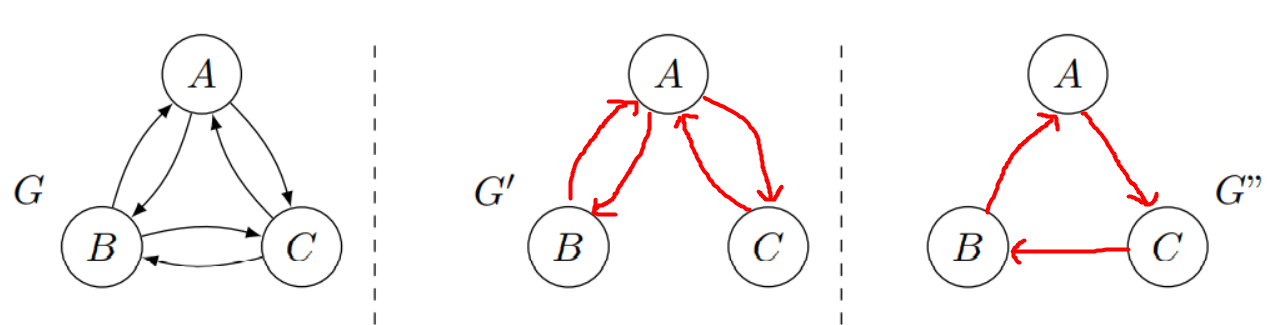
Spanning Subgraph Example 2
Starting from the graph $G$, create:
- $G'$: $\tau$-minimal $\tau$-equivalent
- $G''$: $\tau$-minimum $\tau$-equivalent
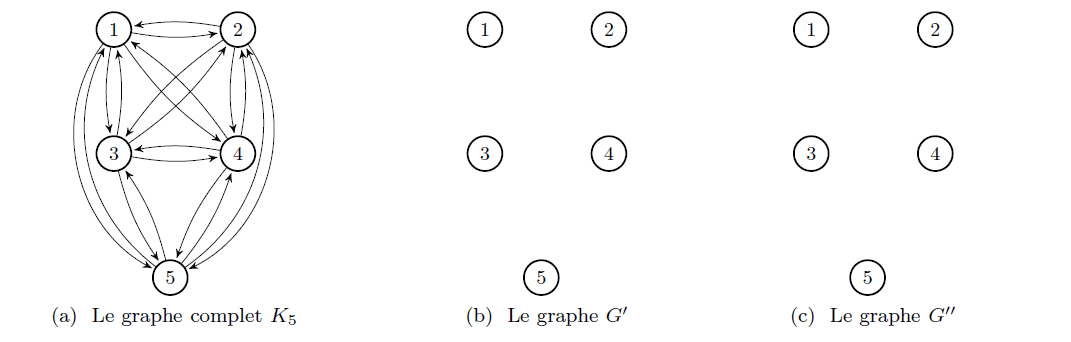
One possible answer: