Trees Example

Spanning Tree Example

Given this graph $G$, give a spanning tree $T$

Spanning Tree Example Graph

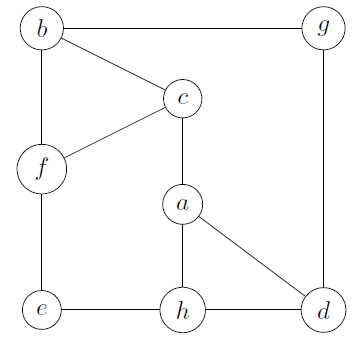
  • we are randomly picking the edges (that we may remove)
    • (b,f) from b,c,f,b
    • (f,e) from f,c,a,h,e,f
    • (h,d) from a,d,h,a
    • (g,d) from a,d,g,b,c,a
  • we are checking if this is a tree (acyclic and connected)
  • we are good
  • our spanning tree is

Spanning Tree Example Result

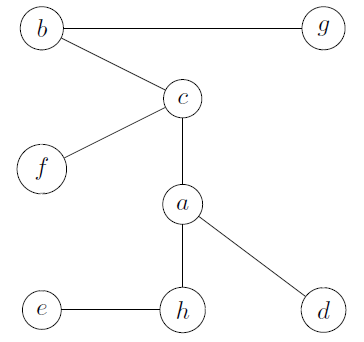
Another answer: $(b,f),(e,h),(h,d),(b,g)$.

Minimum Weight Spanning Tree Kruskal Example

The cost of constructing a road from "N" (Neuilly) to "Châtelet" is represented by the value located at the intersection of the "Châtelet" row and the "N" column. Create a tree from this table.

Minimum Weight Spanning Tree Kruskal Example Table

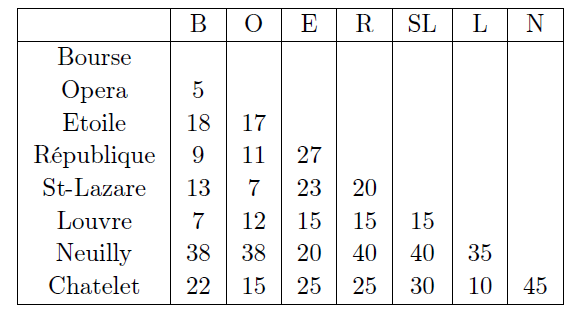
We are creating eight vertices for our eight destinations. We create the smallest cost. It's 5. If adding B (Bourse) - Opera is creating a cycle,

  • then we do not add it to the graph
  • otherwise, we add it to the graph

We repeat this process until all nodes are connected.

Minimum Weight Spanning Tree Kruskal Example Tree

Minimum Weight Spanning Tree Prim Example

Apply Prim's algorithm on this graph, starting from a.

Minimum Weight Spanning Tree Prim Example Graph

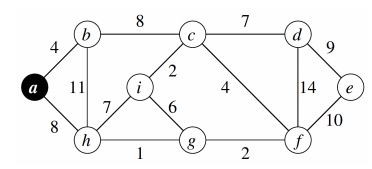
I colored in red the edges we may pick. Then, among the ones in red, I try to add one with the least weight. I colored in blue the one I picked. If I can't pick an edge, I colored it in grey.

Minimum Weight Spanning Tree Prim Example GIF

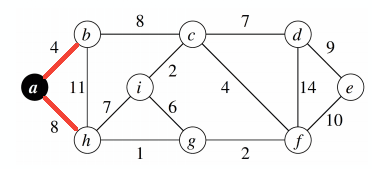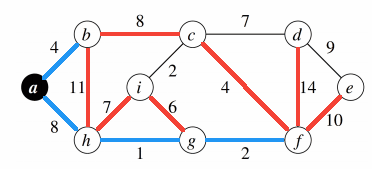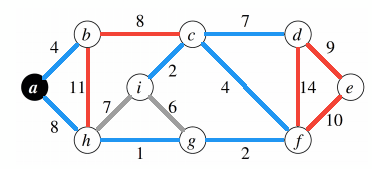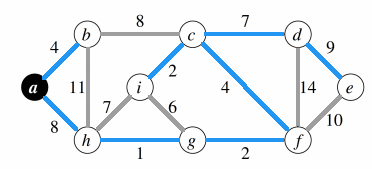
Some may pick $b-c$ instead of $a-h$, since both weights are $8$. I picked $a-h$ and it doesn't matter. The rest of the graph would be the same aside from this one edge.

The GIF frame by frame:

Minimum Weight Spanning Tree Prim Example FRAMES