Graph Representations Examples

Adjacency Matrix Examples

Given the following graph:

adjacency matrix example 1

The adjacency matrix is:

\[ \displaylines{ \hspace{0.7cm}\begin{array}{} a&b&c&d&h&i \end{array} \ \ \ \\ \begin{array}{} a\\b\\c\\d\\h\\i \end{array} \begin{pmatrix} 0 & 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix} } \]

Given the following graph:

adjacency matrix example 2

The adjacency matrix is:

\[ \displaylines{ \hspace{0.7cm}\begin{array}{} a&b&c&d&h&i \end{array} \ \ \ \\ \begin{array}{} a\\b\\c\\d\\h\\i \end{array} \begin{pmatrix} 0 & 1 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ \end{pmatrix} } \]

Incidence Matrix Example

Given the following graph:

incidence matrix example 2

The incidence matrix is:

\[ \displaylines{ \hspace{0.7cm}\begin{array}{}\ a&\ \ \ b&\ \ \ c&\ \ \ d&\ \ \ h&i \end{array} \ \ \ \\ \begin{array}{} a\\b\\c\\d\\h\\i \end{array} \begin{pmatrix} 0 & 1 & -1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & -1 & 0 & 1 \\ -1 & -1 & 1 & 0 & 1 & 0 \\ 0 & -1 & 0 & -1 & 0 & 1 \\ 0 & 0 & -1 & 0 & 1 & 0 \\ \end{pmatrix} } \]

Transitive closure Example

Example 1 (Roy-Warshall algorithm)

Given the following graph:

Transitive Closure Example 1

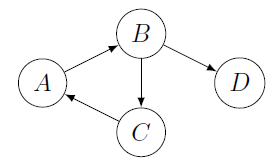
Apply the Roy-Warshall algorithm.

  • picking A
  • $p=C$, $s=B$, creating (C, B)? yes
  • picking B
  • $p=A$, $s=D$, creating (A, D)? yes
  • $p=A$, $s=C$, creating (A, C)? yes
  • $p=C$, $s=D$, creating (C, D)? yes
  • picking C
  • $p=B$, $s=A$, creating (B, A)? yes
  • $p=A$, $s=B$, creating (A, B)? no
  • picking D
  • done

Example 2 (Roy-Warshall algorithm)

Given the following adjacency matrix with $V=\lbrace A, B, C, D\rbrace$:

\[ \begin{pmatrix} 0&1&1&0\\ 1&0&0&1\\ 0&0&0&1\\ 0&1&0&0 \end{pmatrix} \]

Apply the Roy-Warshall algorithm. 💡 Predecessors are in the column and successors are in the line of the vertex we picked.

  • picking A
  • $s=B$, $p=B$? creating (B, B)? no
  • $s=C$, $p=B$? creating (B, C)? yes
  • picking B
  • $s=A$
    • $p=A$? creating (A, A)? no
    • $p=D$? creating (D, A)? yes
  • $s=C$
    • $p=A$? creating (A, C)? no
    • $p=D$? creating (D, C)? yes
  • $s=D$
    • $p=A$? creating (A, D)? yes
    • $p=D$? creating (D, D)? no
  • picking C
  • $s=D$
    • $p=A$? creating (A, D)? no
    • $p=B$? creating (B, D)? no
    • $p=D$? creating (C, D)? no
  • picking D
  • $s=A$, $p=C$? creating (C, A)? yes
  • $s=B$, $p=C$? creating (C, B)? yes
  • $s=B$, $p=C$? creating (C, B)? yes